3.3 Sistemas de ecuaciones
Sistemas de ecuaciones lineales
-
Se denomina sistema de dos ecuaciones lineales con dos variables a dos ecuaciones de este tipo que puedan reducirse a la forma siguiente:
\( a_1x + b_1y = c_1 \)
\( a_2x + b_2y = c_2 \)
- Donde \( a_1, a_ 2, b_ 1, b_ 2, c_ 1, c_ 2 \), son números reales y \( a_1, a_ 2, b_ 1, b_ 2 \) no son simultáneamente cero.
Las ecuaciones que pueden reducirse a la forma \( ax + by = c \) donde \( x \) y \( y \) son variables reales ( con \( a \) , \( b \) y \( c \) números reales dados), tales que \( a \) y \( b \) no sean simultáneamente nulos se llaman ecuaciones lineales con dos variables. El lugar geométrico de los puntos que satisfacen una ecuación de esa forma, es una recta en el plano.
Los métodos para la resolución de sistemas de ecuaciones lineales con dos variables fueron estudiados anteriormente.
- Resolver un sistema de dos
ecuaciones lineales con dos variables es hallar los pares ordenados \( (x;y) \)
que satisfacen simultáneamente las dos ecuaciones.
\( a_1x + b_1y = c_1 \)
\( a_2x + b_2y = c_2 \)
Dichos pares ordenados forman el conjunto solución del sistema.
Si dos sistemas tienen el mismo dominio de definición y el mismo conjunto solución, se llaman equivalentes .
Las transformaciones equivalentes consisten en intercambiar dos ecuaciones, multiplicar una ecuación por un factor diferente de cero o en adicionar un múltiplo constante de una ecuación a otra, con el propósito de eliminar una de las incógnitas.
Ejemplo 1:
En una primera etapa de una competencia de tiro la razón de los puntos obtenidos por Alberto y Enrique es de 10 a 13. Si en la segunda etapa Alberto acumula 10 puntos más, y Enrique 4, entonces estarán empatados. ¿Cuántos puntos obtuvieron Alberto y Enrique en la primera etapa.
Resolución:Como se aprecia, resulta conveniente introducir variables. Para comparar los puntos obtenidos en la primera y segunda etapa vamos a hacer una tabla:
| Puntos obtenidos por:
|
Primera etapa
|
Segunda etapa
|
| Alberto
|
x
|
x +10
|
| Enrique
|
y
|
y + 4
|
En el problema se dan dos relaciones:
La razón de los puntos obtenidos por Alberto y Enrique es de 10 a 13 se expresa como:
\( \frac{x}{y} = \frac{10}{13} \) (I)Si en la
segunda etapa Alberto y Enrique acumulan los puntos que se plantean, estarán
empatados. Esto se representa como:
\( x + 10 = y + 4 \) (II)
Luego,
podemos plantear un sistema de dos
ecuaciones lineales en dos variables para determinar el valor de las
incógnitas.
\( \frac{x}{y} = \frac{10}{13} \) (I)
\( x + 10 = y + 4 \) (II)
Este sistema se transforma en:
\( 13x - 10y = 0 \) (I´)\( x - y = -6 \) (II´)
Tratemos de resolver este sistema de ecuaciones aplicando el método de sustitución:
Obviamente resulta más fácil despejar \( x \) o \( y \) en la ecuación (II):
\( x = y – 6 \) (III)Sustituyendo (III) en (I), resulta:
\( 13(y – 6) – 10y = 0 \)Resolviendo la ecuación anterior:
\( 13y – 78 – 10y = 0 \)
\( 3y = 78 \)
\( y = 26 \)
Conviene entonces sustituir el valor hallado de y en la ecuación (III) y se obtiene que x =26 – 6 = 20.
Comprobando en las dos ecuaciones originales, se verifica que:
| Ecuación (I) | Ecuación (II) |
|
| \( \frac{20}{26} = \frac{10}{13} \)
|
20 + 10 = 26 + 4 |
|
| \( \frac{10}{13} = \frac{10}{13} \)
|
30 = 30 |
|
Además se aprecia que los valores obtenidos por Alberto y Enrique son razonables porque están en la relación 10 a 13. Como 10 y 13 son primos, no podrían ser menores que 10.
Respuesta: En la primera etapa Alberto y Enrique acumularon 20 y 26 puntos respectivamente.
En resumen, hemos procedido de la manera siguiente en la aplicación del método de sustitución :-
- Despejamos una de las variables en una de las ecuaciones.
- Sustituimos la variable despejada en la otra ecuación y de esta forma obtenemos una ecuación en la que aparece una sola variable.
- Resolvemos esta ecuación para obtener el valor de una de las variables.
- Sustituimos el valor hallado en una de las ecuaciones, preferiblemente en la ecuación despejada, para obtener el valor de la otra variable.
Ejemplo:
Resolver el sistema anterior por el método de adición-sustracción:
\( 13x - 10y = 0 \) (I´)\( x - y = -6 \) (II´)
Multiplicando (II´) por –10 se obtiene:
\( 13x - 10y = 0 \) (I´)
\( -10x + 10y = 60 \) (II´)
\( \begin{equation} \cfrac{13x - 10y = 0 \hspace{3mm} (I´)\\ -10x + 10y = 60 \hspace{3mm} (II´)}{3x = 60\\x=20} \end{equation} \)
De manera análoga a como se hizo anteriormente se sustituye el valor hallado de x en una de las ecuaciones, digamos en (II´), y se obtiene que y =26.
En resumen, hemos procedido de la
manera siguiente en la aplicación del método
de adición-sustracción o método aditivo.
-
- Transformamos convenientemente las ecuaciones del sistema de manera que obtengamos dos ecuaciones, de modo que los coeficientes de una de las variables sean iguales u opuestos.
- Sustraemos o adicionamos según convenga, miembro a miembro, las ecuaciones del sistema transformado, para obtener una ecuación en una sola variable.
- Hallamos la solución de dicha ecuación .
- Sustituimos el valor obtenido de la variable en una de las ecuaciones del sistema original según convenga, para hallar el valor de la otra variable.
La escritura del conjunto solución no siempre es necesaria de acuerdo con las exigencias del ejercicio o problema.
La comprobación, debe realizarse en todas las situaciones, sean ejercicios formales o problemas.
Ejemplo 2
Halla el conjunto solución de los sistemas de ecuaciones lineales que se dan a continuació.a) \( \begin{cases} 7y -15x = 1 (I) \\ -y - 6x = 8 (II) \end{cases} \) b) \( \begin{cases} 4x + \frac{8}{5}y = \frac{4}{5} (I) \\ 5x - 2x = 9 (II) \end{cases} \) c) \( \begin{cases} -4x + \frac{8}{5}y = \frac{4}{5} (I) \\ 5x - 2y = -1 (II) \end{cases} \)
Resolución:
a) Si este sistema se resuelve por el método de adición – sustracción resulta más fácil eliminar la variable \( y \), debido a que en ambas ecuaciones tiene signos opuestos. Luego si multiplicamos la ecuación (II) por 7 se obtiene:
\( \begin{cases}7y - 15x = 1 \\ -7y - 42x = 56 \end{cases} \)Ahora, adicionando ambas ecuaciones miembro a miembro se obtiene \( -57x = 57 \) de donde resulta \( x = –1 \). Para hallar el valor de \( y \) se sustituye en cualquiera de las ecuaciones y se obtiene \( y = –2 \)
Comprobación:
| En la ecuación (I) | En la ecuación (II) |
|
|
|
|
\( 7y – 15x = 1 \)
|
\( –y – 6x = 8 \)
|
|
MI: \( 7y – 15x \\ =7(–2) –15(–1) \\ = –14 + 15 \\ = 1 \)
|
MI: \( –(–2) – 6(–1) \\ = +2 + 6 \\ = 8 \)
|
| MD: 1 | MD: 8 |
| MI = MD | MD = MI |
Interpretación geométrica de la solución:
Se trata de las rectas, que son las gráficas de las funciones lineales cuyas ecuaciones son \( y = \frac{15}{7}x + \frac{1}{7} \) y \( y = -6x - 8 \); en este caso las rectas se interceptan en el punto \( (-1; -2) \). Observa que las pendientes de las rectas son diferentes.
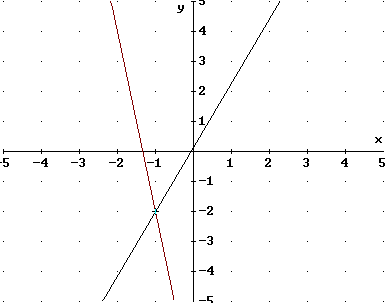
¿Qué sucede cuando las pendientes son iguales?
Aplicando el método de adición – sustracción se puede multiplicar ambas ecuaciones por un valor diferente de cero o multiplicar la ecuación (I) por \( \frac{5}{4} \), en este caso resulta:
\( \frac{\begin{cases} -5x+2y=1 \hspace{3mm} (I ) \\ 5x-2y=9 \hspace{3mm} (II) \end{cases}}{0y + 0y = 10} \)De manera evidente se aprecia que el resultado obtenido es una contradicción, luego este sistema no posee solución alguna. Por tanto, \( S = \lbrace{ }\rbrace \)
Significado geométrico de la solución del sistema:Se trata de las funciones lineales dadas por las ecuaciones \( y= \frac{5}{2}x + \frac{1}{2} \) y \( y= \frac{5}{2}x - \frac{9}{2} \) que tienen igual pendiente (\( m = \frac{5}{2} \)) y diferente términos independientes (\( \frac{1}{2} \neq -\frac{9}{2} \)). Esto significa que se trata de dos rectas paralelas.
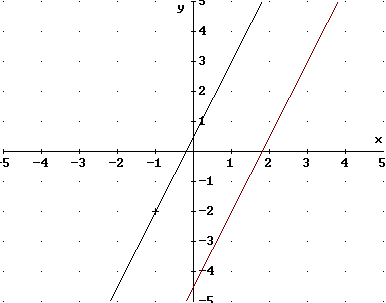
c) \( \begin{cases} -4x + \frac{8}{5}y = \frac{4}{5} (I) \\ 5x - 2y = -1 (II) \end{cases} \)
Resolviendo el sistema de forma análoga al inciso b), obtenemos:
\( \frac{\begin{cases} -5x + 2y = 1 \hspace{3mm} (I)\\ 5x -2y = -1 \hspace{3mm} (II)\end{cases}}{0x + 0y = 0} \)
Se aprecia que hemos obtenido un sistema formado por dos ecuaciones equivalentes. Una se obtiene de otra multiplicando por (–1) una de ellas. De modo que los infinitos pares ordenados \( (x; y) \) que satisfacen una cualquiera de estas ecuaciones, serán solución del sistema, por tanto, el sistema tiene infinitas soluciones.
\( S = \lbrace{(x, y): x \in \mathbb{R} , y \in \mathbb{R}, 5x -2y = -1 }\rbrace \)
Significado geométrico de la solución del sistema:
Se trata de dos funciones lineales dadas por la misma ecuación \( y= \frac{5}{2}x + \frac{1}{2} \) por tantos sus gráficas son dos rectas coincidentes.
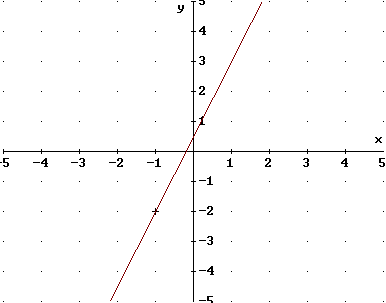
Un sistema puede tener solución única, no tener soluciones o tener infinitas soluciones, en dependencia de si las rectas correspondientes a cada una de las ecuaciones del sistema se cortan, son paralelas o coincidentes como se ilustra en el ejemplo anterior.
Para determinar analíticamente, si el sistema
\( \begin{cases}
a_1x + b_1y =c_1\\ a_2x + b_2y =c_2
\end{cases} \)
\( \begin{cases} y = - \frac{a_1}{b_1} x - \frac{c_1}{b_1} \\ y = - \frac{a_2}{b_2} x - \frac{c_2}{b_2} \end{cases} \)
De acuerdo con el valor de las pendientes y del intercepto con el eje de las ordenadas de las rectas correspondientes a cada una de las ecuaciones del sistema, tenemos:
-
1. Si \( - \frac{a_1}{b_1} \neq \frac{a_2}{b_2} \) entonces el sistema tiene una única solución, porque las rectas se cortan.
2. Si \( - \frac{a_1}{b_1} = \frac{a_2}{b_2} \) (I) y \( - \frac{c_1}{b_1} = \frac{c_2}{b_2} \) (II) el sistema no tiene solución, porque las rectas son paralelas.
3. Si \( - \frac{a_1}{b_1} = \frac{a_2}{b_2} \) (I) y \( - \frac{c_1}{b_1} = \frac{c_2}{b_2} \) (II) entonces el sistema tiene infinitas soluciones, porque las rectas son coincidentes.
Explica con tus palabras el significado de las igualdades que aparecen en el recuadro anterior y comprueba estos resultados con los obtenidos en el ejemplo 2.
La interpretación geométrica de un sistema de dos ecuaciones lineales con dos variables, de la forma:\( \begin{cases} a_1x + b_1y =c_1\\ a_2x + b_2y =c_2 \end{cases} \)
se puede realizar de manera muy práctica a partir de los coeficientes de las variables.
| Relación entre los coeficientes |
Relación entre las rectas |
Conjunto solución |
|---|---|---|
| \( \frac{a_1}{a_2} \neq \frac{b_1}{b_2} \) | Las rectas se interceptan en un punto \( P(x; y) \) |
\( S = \lbrace{(x; y)}\rbrace \) |
| \( \frac{a_1}{a_2} = \frac{b_1}{b_2} \neq \frac{c_1}{c_2} \) | Las rectas son paralelas | \( S = \lbrace{}\rbrace \) |
| \( \frac{a_1}{a_2} = \frac{b_1}{b_2} = \frac{c_1}{c_2} \) | Las rectas son coincidentes |
Infinitas soluciones |
Ejemplo 3
Sea el sistema:
\( \begin{cases} ay - (2a + b)x =b \\ -y -(a-b)x = a+b \end{cases} \)
Determina el valor de los parámetros \( a \) y \( b \), para que el conjunto solución del sistema sea \( S = \lbrace{( –2; –1)}\rbrace \)
Resolución:
Como nos dan el conjunto solución del sistema, entonces los valores numéricos de las variables son \( x = –2 \) y \( y = −1 \), los cuales deben satisfacer simultáneamente a las dos ecuaciones del sistema. Sustituyendo estos valores en las ecuaciones y realizando las operaciones indicadas, se obtiene un sistema de ecuaciones en las variables \( a \) y \( b \) :
\( \begin{cases} -a + 2(a+b) = b \hspace{3mm} (I) \\ 1+2(a-b) = a+b \hspace{3mm} (II) \end{cases} \)
Efectuando se obtiene:
\( \begin{cases} 3a + b = 0 \hspace{3mm} (I´) \\ a - 3b = -1 (II´) \end{cases} \)
Despejando en (I´) \( b = –3a \) y sustituyendo en (II´) resulta:
\( a–3(–3a) = –1 \)
\( a+9a = –1 \)
\( a=–0,1 \)
En consecuencia, \( b = 0,3 \)
Luego los valores de \( a \) y \( b \) son –0,1 y 0,3 respectivamente.