Inecuación fraccionaria

• Una inecuación fraccionaria es una inecuación de la forma:
  

  \( \frac{A}{B} > 0, \frac{A}{B} < 0, \frac{A}{B} \geq 0, \frac{A}{B} \leq 0 \) donde \( A \) y \( B \) son polinomios y en \( B \) aparece al menos una variable. 

¿Cómo resolver inecuaciones fraccionarias?

• 1) Se transponen todos sus términos y se compara con cero.
  2) Se realizan las operaciones indicadas y se reducen los términos semejantes.
  3) Si hay factores comunes en el numerador y el denominador se pueden simplificar teniendo en cuenta que los ceros de los factores simplificados hay que excluirlos del conjunto solución. En caso que no se simplifique es necesario considerar los ceros dobles, en los cuales no hay cambios de signos en la recta numérica.
  4) Se hallan los ceros del numerador y del denominador.

• 5) Se traza una recta numérica y se sitúan los ceros en orden ascendente de izquierda a derecha, marcar si los ceros se incluyen o no en la desigualdad teniendo en cuenta que los ceros del denominador siempre se excluyen porque no son valores del dominio de la fracción.
  6) Si los coeficientes de las variables de mayor grado tienen el mismo signo, los signos de los intervalos que se determinan irán variando de forma alternada de derecha a izquierda comenzando por el positivo.
  7) Si alguno de los coeficientes de la variable de mayor grado tiene signo negativo, se multiplica por (-1) ambos miembros de la inecuación, es decir , se cambian los signos de los coeficientes del polinomio de mayor grado que tiene coeficiente negativo, se cambia el sentido de la desigualdad y se reduce este caso al anterior.
  8) Se selecciona los intervalos que satisfacen la inecuación y se escribe el conjunto solución teniendo en cuenta que los ceros del numerador pueden o no incluirse, en dependencia de que la desigualdad tenga o no incluida la igualdad (≤,   ≥).

Ejemplo 1

Resuelve las siguientes inecuaciones:

a) \( \frac{x+1}{x-1} > 0 \) b) \( \frac{x+2}{4(x-3)} \leq 0 \) c) \( \frac{x^2-5x-36}{x^2-4} < 0 \) d) \( \frac{(x-5)^2}{(x+3)(1-x)} > 0 \)

Soluciones:

a) \( \frac{x+1}{x-1} > 0 \)  En este caso es necesario determinar los valores de la variable para los cuales el cociente es mayor (estricto) que cero, luego es necesario hallar los ceros de las funciones que aparecen en el numerador y en el denominador.

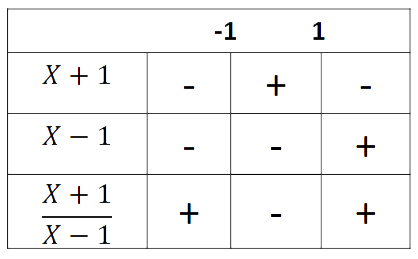
luego la solución son \( x \in \mathbb{R}: x \in ( \infty; 1 ) \cup (1; \infty ) \)

b) \( \frac{x+2}{4(x-3)} \leq 0 \) En este caso se trata de analizar cuales son los valores de la variable que hacen al cociente, no positivo

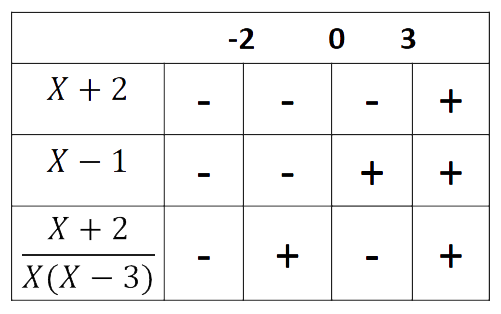
Gráficamente obtenemos:

 

Entonces la solución es:
\( x \in \mathbb{R}: x \in ( \infty; -2] \cup (0;3) \)

 
c) \( \frac{x^2-5x-36}{x^2-4} < 0 \) En este caso es necesario buscar los valores de la variable para los cuales el cociente es negativo, pero se debe observar que la expresión del denominador siempre es positiva, o sea es la expresión de una función cuadrática cuyo grafico  es una  parábola que tiene su vértice en [0; 4], luego no intercepta al eje \( x \). En este ejemplo se realizara el análisis de signo directamente atendiendo a la descomposición de factores realizada y a las pendientes de las funciones que aparecen:
\( \frac{(x-9)(x+4)}{x^2+4} < 0 \)

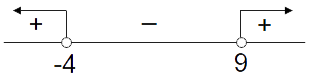
entonces los valores que hacen al cociente negativo son \( x \in \mathbb{R}: x \in (-4; 9) \)
d) \( \frac{(x-5)^2}{(x+3)(1-x)} > 0 \)

Se debe observar en la inecuación que:

• En el numerador hay un cero doble porque la expresión corresponde a una parábola con vértice en el punto (-5 ; 0) luego siempre es positiva excepto en \( x = 5 \) que toma valor cero.

• En el denominador hay una función lineal de pendiente negativa, lo que indica que en el análisis de signo se debe comenzar de derecha a izquierda con el signo menos o multiplicar la inecuación por -1 y cambiar el signo de la desigualdad.

 

\( x \in \mathbb{R}: x \in (-3; 1) \cup \lbrace{5}\rbrace \)
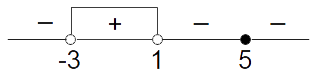
Ejemplo 2
Halla el conjunto solución de la siguiente inecuación \( \frac{4x-1}{2x-3} \leq 1 \)
Para resolver la inecuación es necesario transferir el uno para el miembro izquierdo, es decir  restar 1 en cada miembro, luego
\( \frac{4x-1}{2x-3} - 1 \leq 0 \) Ahora hay que buscar el denominador común
\( \frac{4x-1-2x+3}{2x-3} \leq 0 \) Se reduce términos semejantes y se obtiene
\( \frac{2x+2}{2x-3} \leq 0 \) para realizar el análisis de signo se deben factorizar las expresiones si es posible
\( \frac{2(x+1)}{2x-3} \leq 0 \)

la solución de la inecuación es  \( x \in \mathbb{R}: x \in [-1; 1,5) \)

Ejemplo 3

Determina para qué valores reales de la variable no están definidas las siguientes expresiones:

a) \( \sqrt[]{\frac{1-x^2}{x^2} } \) b) \( \sqrt[]{\frac{4x-3}{x} } \)

A partir de la definición de radicación se conoce que la radicación de índice par esta definida en el conjunto de los números reales si y solo si  el argumento es mayor e  igual a cero, esto significa que no está definida si este el menor que cero, luego:
Solución:
Si a) \( \sqrt[]{\frac{1-x^2}{x^2} } \) entonces \( \frac{1-x^2}{x^2} < 0 \) se procede a factorizar para realizar el análisis de signo \( \frac{(1-x)(x+1)}{x^2} < 0 \)

entonces la expresión no está definida para  \( x \in \mathbb{R} : x \in ( \infty; -1 ) \cup (1; \infty ) \)

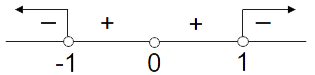
b) \( \sqrt[]{\frac{4x-3}{x} } \) la expresión no está definida si \( \frac{4x-3}{x} < 0 \)
Luego, los valores que indefinen la expresión son \( x \in \mathbb{R} : 0 < x < \frac{3}{4} \)