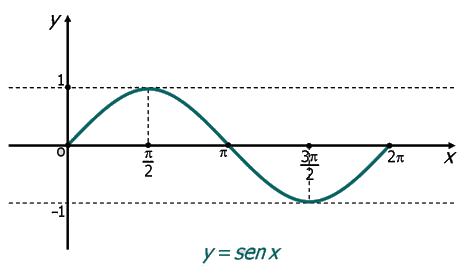
La función \( f(x) = sen(x) \)(Función seno)

Función seno

• La correspondencia que a cada número real \( x \) le asocia \( sen(x) \) se denomina función seno. Se puede escribir como:
  

• \( f = \lbrace{(x;y) : y= sen x}\rbrace \)
  

• 
  

• Propiedades

  Domf: \( x \in \mathbb{R} \)

• Imf: \( -1 \leq x \leq 1 \) 

  Ceros: \( x = k \Pi, k \in \mathbb{Z} \)

  Por tanto los ceros de la función en el intervalo principal son : \( 0; \Pi; 2 \Pi \)

  Monotonía: No es monótona. Crece y decrece por intervalos.

  Inyectividad: No es inyectiva.

  Paridad: Es impar.

  Periodicidad: Es periódica y cualquier múltiplo entero de \(  2 \Pi \) es un período de la función. El periodo principal es \( 2 \pi \)

  Valor máximo o mínimo: Valor Máximo \( y_0 = 1 \); Valor Mínimo \( y_0 = -1 \);    
  

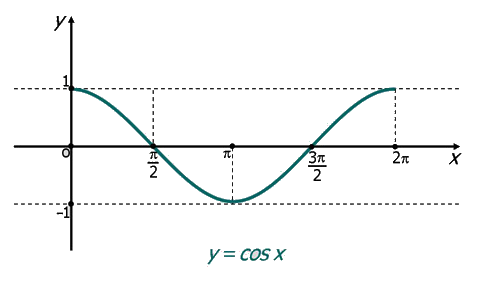
La función \( f(x) = \cos(x) \) (Función coseno)

Función coseno

• La correspondencia que a cada número real \( x \) le asocia cosx se denomina función coseno. Se puede escribir como:
  

• \( f = \lbrace{(x;y):y = \cos x, x \in \mathbb{R}}\rbrace \)
  

• 
  

• Propiedades

• Domf: \( x \in \mathbb{R} \)

• Imf: \( -1 \leq x \leq 1 \) 

  Ceros: \( x= (2k + 1) \) \( \frac{ \Pi }{2} \), \( k \in \mathbb{Z}\)  

  Por tanto los ceros de la función en el intervalo principal son: \( \frac{\Pi}{2} \)  y \( \frac{3\Pi}{2} \) 
  

  Monotonía: No es monótona. Se alternan intervalos de crecimiento y decrecimiento

  Inyectividad: No es inyectiva

  Paridad: Es par

  Periodicidad: Es periódica y cualquier múltiplo entero de \( 2\Pi \) es un período de la función.  El periodo principal es \( 2 \pi \)

  Valor máximo o mínimo: Valor Máximo \( y_0 = 1 \); Valor Mínimo \( y_1 = -1 \)       

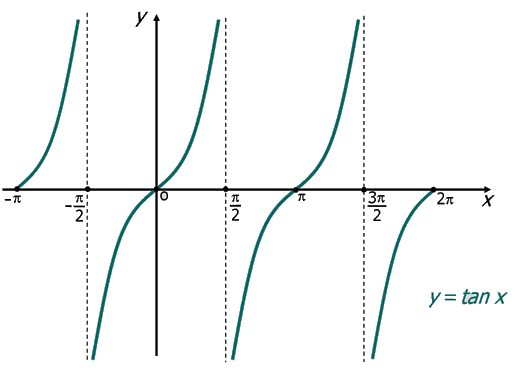
La función \( f(x) = \tan(x) \) (Función tangente)

Función tangente

• La correspondencia que a cada número real \( x \) tal que \( x \neq (2k + 1) \frac{\Pi}{2}, k \in \mathbb{Z} \) le asocia \( \tan( x) \) se denomina función tangente. Se puede escribir como: 
  

• \( f = \lbrace{(x;y) : y= \tan x, x \in \mathbb{R} , x \neq (2k + 1) \frac{\Pi}{2}, k \in \mathbb{Z} }\rbrace \)
  

• 
  

• Propiedades

   Domf: \( x \in \mathbb{R} , x \neq (2k+1) \frac{\Pi}{2} , k \in \mathbb{Z} \)

   Imf: \( y \in \mathbb{R} \) 

  Ceros:   \( x= k\Pi, k \in \mathbb{Z} \)

  Por tanto el cero de la función en el intervalo principal son 0, \( \pi \) y \( 2 \pi \)

  Monotonía: No es monótona. En cada intervalo que no contiene puntos de indefinición es creciente.

  Inyectividad: No es inyectiva.

  Paridad: Es impar.

• Periodicidad: Es periódica y cualquier múltiplo entero de \( \Pi \) es un período de la función.  El periodo principal es \( \pi \)

  Valor máximo o mínimo: No tiene valor máximo ni mínimo.       
  

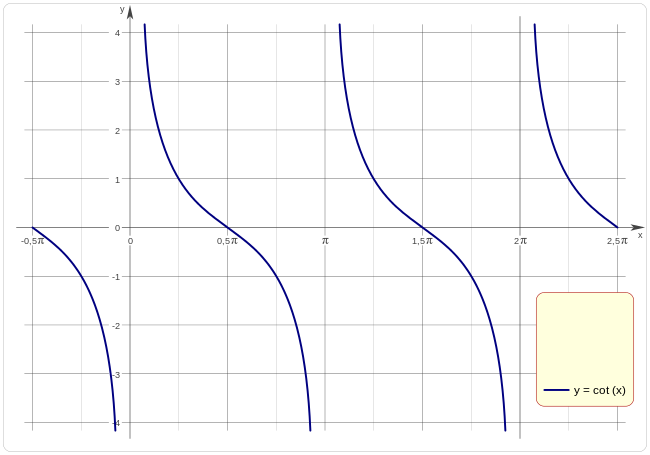
La función \( f(x) = \cot(x) \) (Función cotangente).

Función cotagente

• La correspondencia que a cada número real \( x \) tal que \( x \neq k\Pi \) se  asocia \( \cot x \) se denomina función cotangente. Se puede escribir como: 
  

• \( f = \lbrace{(x;y) : y= \cot x, x \in \mathbb{R} , x \neq k\Pi, k \in \mathbb{Z} }\rbrace \) 

• 

• Propiedades

   Domf: \( \lbrace{x \in \mathbb{R} , x \neq k\Pi, k \in \mathbb{Z}\rbrace a} \) 

   Imf: \( y \in \mathbb{R} \), 

  Ceros:   \( x= (2k+ 1) \frac{\Pi}{2} , k \in \mathbb{Z} \)

  Por tanto el cero de la función en el intervalo en que se representó la función es :  \( \frac{\Pi}{2} \)

  Monotonía: No es monótona. En cada intervalo que no contiene puntos de indefinición es decreciente

  Inyectividad: No es inyectiva.

  Paridad: Es impar.

  Periodicidad: Es periódica y cualquier múltiplo entero de \( \Pi \) es un período de la función.

  Valor máximo o mínimo: No tiene valor máximo ni mínimo.