Un radical esta simplificado cuando:
• El índice no tiene factores comunes con el exponente del radicando.
• Se han extraído los factores que son raíces exactas.
• El radicando no tiene denominador.
Ejemplo:

a) a) \( \sqrt[8]{3^4} \)

En este caso el índice del radical es 8 y el exponente del radicando es 4, observa que tienen un factor común, luego, este radical no está simplificado. Aplicando la propiedad 3) de los radicales resulta: \( \sqrt[8]{3^4} = \sqrt[2 \cdot 4]{3^{1 \cdot 4}} = \sqrt[]{3} \)

b) \( \sqrt[4]{7^9} \)

Este radical no está simplificado porque en el radicando hay factores que son raíces exactas. Aplicando la propiedad de potencias de igual base y la propiedad 2) de los radicales se obtiene: 

\( \sqrt[4]{7^9} = \sqrt[4]{7^8} \cdot \sqrt[4]{7} \\=7^2 \cdot \sqrt[4]{7} \\= 49 \sqrt[4]{7} \)

En la práctica, cuando el radicando está elevado a un exponente mayor que el índice del radical, se divide el exponente del radicando por el índice, el cociente es el exponente de la potencia que “sale” del radical, mientras que el resto es el exponente de la potencia que  “queda” en el radical.
En este caso

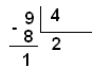
     Luego, \( \sqrt[4]{7^9}=7^2 \cdot \sqrt[4]{7}\\=49 \sqrt[4]{7} \)

c) \( \sqrt[4]{ \frac{a^5}{16x^4}} \)

Este radical en el radicando tiene denominador, entonces no está simplificado. Aplicando la propiedad 6) y la propiedad 1) de los radicales resulta:

\( \sqrt[4]{ \frac{a^5}{16x^4}}= \frac{\sqrt[4]{a^5} }{\sqrt[4]{16x^4} } = \frac{\sqrt[4]{a^5} }{\sqrt[4]{2^4x^4} }= \frac{a\sqrt[4]{a} }{2x} \)