Circunferencia

• Se llama circunferencia al conjunto de todos los puntos del plano situados a la misma distancia de un punto fijo \( O \) de dicho plano. Se denota \( C(O; r) \) y se lee circunferencia de centro \( O \) y radio \( r \).

Cuerda: Segmento que une dos puntos de la circunferencia.
Diámetro: La mayor cuerda que pasa por el centro de la circunferencia.

\( \begin{equation} \overline{CD} \end{equation} \): cuerda

\( \begin{equation} \overline{AB} \end{equation} \): diámetro

Se cumple que: \( d= 2r \) 

 La mediatriz de toda cuerda pasa por el centro de la circunferencia.

\( m \): mediatriz del \( \begin{equation} \overline{AB} \end{equation} \)

\( O \in m \)

Recuerda que:

• -Cada cuerda divide en dos partes a la circunferencia.

  -Los arcos determinados por el diámetro son iguales y cada uno de ellos se llama semicircunferencia.
  

Círculo

• Se llama círculo al conjunto formado por todos los puntos de una circunferencia y sus puntos interiores.

Rectas exteriores: No tienen ningún punto común. La distancia del centro de la circunferencia a la recta es mayor que el radio, \( d(O; e) > r \).

Recta tangente: Tienen un punto común. La distancia del centro de la circunferencia a la recta es igual que el radio, \( d(O; t) > r \).

Recta secante: Tienen dos puntos comunes. La distancia del centro de la circunferencia a la recta es menor que el radio, \( d(O; s) > r \).

Teorema sobre la perpendicularidad de la tangente

• La recta tangente a una circunferencia es perpendicular al radio que tiene como extremo el punto de tangencia. Llamamos a este segmento radio de tangencia.

Recíproco del teorema de la perpendicularidad de la tangente

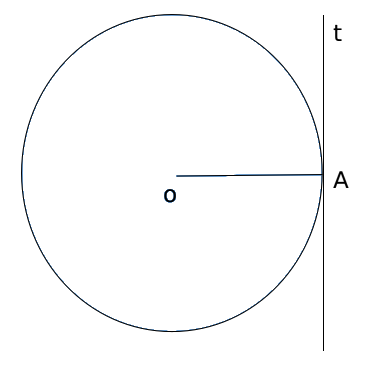
• La recta perpendicular a un radio, en el extremo que pertenece a la circunferencia, es una recta tangente a dicha circunferencia en ese punto.

Ángulos en la circunferencia:

Ángulo central

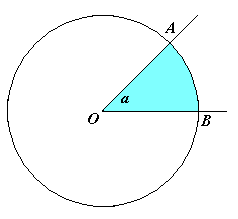
• Un ángulo central es aquel que tiene su vértice en el centro de una circunferencia y sus lados son radios de esta.
• 
  

Recuerda que

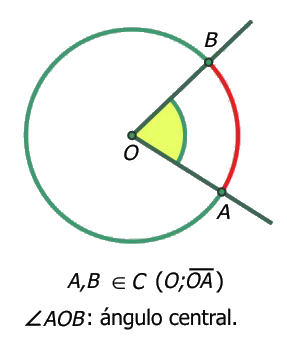
• La definición de arco y cuerda correspondiente a un ángulo central.

• -El arco correspondiente a un ángulo central en una circunferencia, es el arco que determinan sus lados al cortarla y cuyos puntos están contenidos en el interior de dicho ángulo.

• 
  
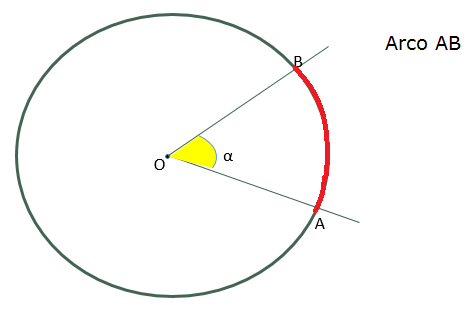
• -La cuerda correspondiente a un ángulo central es el segmento que determinan los puntos de intersección de sus lados con la circunferencia.
• 
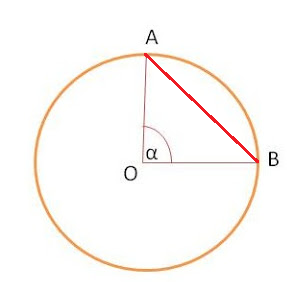
• Cuerda \( \begin{equation} \overline{AB} \end{equation} \)
• 
  

  -La amplitud de un ángulo central es la amplitud de su arco correspondiente y recíprocamente, la amplitud de un arco de circunferencia es la misma que la de su ángulo central.

Teoremas sobre relaciones entre ángulos centrales, arcos y cuerdas:

Teorema (ángulo central y arco)

• En una circunferencia o circunferencias iguales, a ángulos centrales iguales corresponden arcos iguales.

Teorema (arco y ángulo central)

• En una circunferencia o circunferencias iguales, a arcos iguales corresponden ángulos centrales iguales.

Teorema 3 (ángulo central y cuerda)

• En una circunferencia o circunferencias iguales, a ángulos centrales iguales corresponden cuerdas iguales.

Recíproco

• En una circunferencia o circunferencias iguales, a cuerdas iguales corresponden ángulos centrales iguales.

Ángulos inscritos en la circunferencia:

Ángulo inscrito

• El ángulo formado por la unión de dos semirrectas de origen común, cuyo vértice pertenece a una circunferencia y cuyos lados intersecan a la circunferencia en otros dos puntos se denomina ángulo inscrito a la circunferencia.

 

Teorema

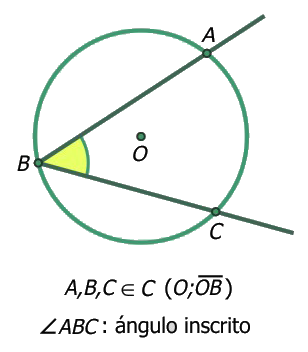
• La amplitud de un ángulo inscrito en una circunferencia es igual a la mitad de la amplitud de su arco correspondiente.
• 
• \( \sphericalangle APB = \frac{\stackrel{\textstyle\frown}{\mathrm{AB}}}{2} \)
  

Teorema

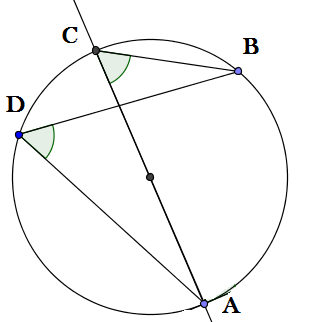
• Los ángulos inscritos en una circunferencia a los cuales les corresponde el mismo arco son iguales.
• 
  

Teorema de Tales

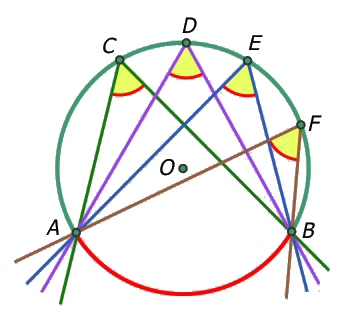
• Si a un ángulo inscrito en una circunferencia le corresponde un arco que es una semicircunferencia o su cuerda correspondiente es un diámetro, entonces es un ángulo recto.

 

Recíproco del Teorema de Tales

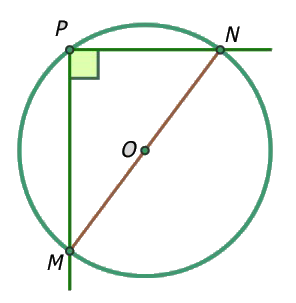
• Si un ángulo inscrito en una circunferencia es recto, entonces su arco correspondiente es una semicircunferencia y la cuerda correspondiente es un diámetro.

Teorema relación ángulo central - ángulo inscrito

• Si a un ángulo central y a un ángulo inscrito en una circunferencia les corresponde el mismo arco, entonces la amplitud del ángulo inscrito es igual a la mitad de la amplitud del ángulo central.
• 
  

Ángulos seminscritos

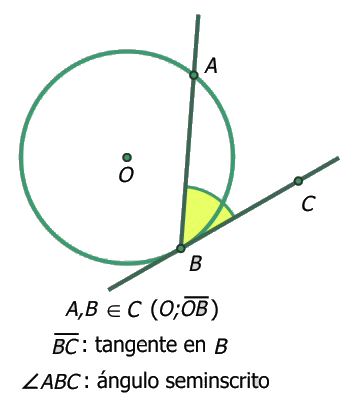
• El ángulo formado por la unión de dos semirrectas de origen común, cuyo vértice pertenece a una circunferencia y cuyos lados son uno tangente y el otro secante a dicha circunferencia se denominan ángulo seminscrito a la circunferencia.
• 
  

Teorema sobre la amplitud del ángulo seminscrito

• La amplitud de un ángulo seminscrito en una circunferencia es igual a la mitad de la amplitud de su arco correspondiente.

Teorema (relación ángulo central, inscrito y seminscrito)

• -Si a un ángulo inscrito y a un ángulo seminscrito en una circunferencia les corresponde el mismo arco, entonces sus amplitudes son iguales.
  
  -Si a un ángulo inscrito o a un ángulo seminscrito en una circunferencia les corresponde el mismo arco que a un ángulo central, entonces la amplitud del ángulo inscrito o seminscrito es igual a la mitad de la amplitud del ángulo central.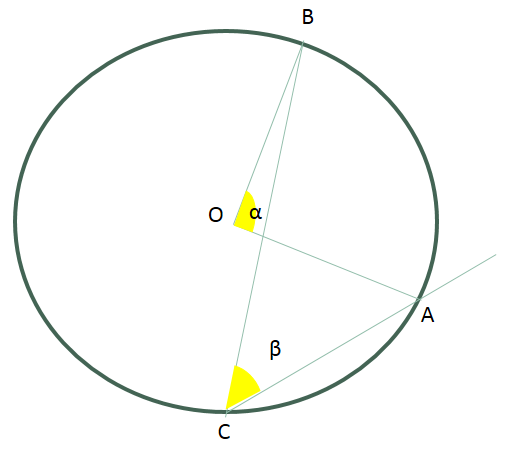
• 
• \( \alpha \): ángulo central
• \( \beta \): ángulo inscrito
• \( \beta = \frac{\alpha}{2} \)
  

Polígono inscrito

• Un polígono esta inscrito en una circunferencia cuando todos sus vértices son puntos de dicha circunferencia.
• 
  

Polígono circunscrito

• Un polígono esta circunscrito en una circunferencia si sus lados son tangentes a dicha circunferencia.
• 
  

Todo polígono regular se puede inscribir y circunscribir a una circunferencia.

Longitud de la circunferencia: \( L = 2 \pi r \) o \( L = \pi d \)

Área del círculo: \( A_{c} = \pi r^2 \)

Área del sector circular: \( A_{sc} = \frac{A_{c}\cdot \alpha^0 }{360^0} \) (sector circular: Conjunto de puntos del círculo limitada por los lados de un ángulo central y su arco correspondiente).